Влияние шумов и помех

2.1.1 Влияние шумов и помех

Шумы определяют емкость канала и задают частоту ошибок при передаче цифровых данных. Шум по своей природе нестабилен и можно говорить лишь о том, что его величина с некоторой вероятностью лежит в определенном интервале значений. Плотность вероятности p(x) определяет вероятность того, что случайный сигнал X имеет значение амплитуды в интервале между x и x+Dx. При этом вероятность того, что значение х лежит в интервале между x1 и x2 определяется равенством:

, условием нормировки при этом является равенство

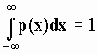
P(x) – вероятность, а p(x) – плотность вероятности. Вероятность того, что x меньше некоторой величины y равна

, откуда следует, что P{x1 2} = P(x2) – P{x1}, а

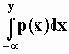
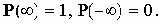
Так называемый белый шум подчиняется непрерывному нормальному (Гауссову) распределению

, где а – среднее значение x, а s – среднеквадратичное отклонение х от a. В случае шумов среднее значение х с учетом полярности часто принимает нулевое значение (а=0).

В этом случае, если мы хотим знать вероятность того, что амплитуда шумового сигнала лежит в пределах ±

v, то можно воспользоваться выражением

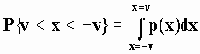
Для вычисления P{x1<x<-x1} обычно используются равенства

. Тогда P{x11} =

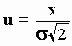
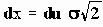
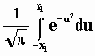
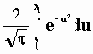
Распределение P(x) обычно называется функцией ошибок (erf(x) = -erf(-x)). Полезной с практической точки зрения является вероятность

P{-kss}=Pk(k s) =

, которая позволяет оценить возможность того, что шумовой сигнал превысит некоторый порог, заданный значением k.

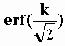
Из числа дискретных распределений наиболее часто используемым является распределение Пуассона.

, где n = 0, 1, 2, …; a=mP, m – число испытаний. Распределение Пуассона описывает вероятность процессов, где Pm отношение n/m приближается к значению вероятности P.

Среднее значение x

, а для дискретного распределения

. Среднеквадратичное отклонение s случайной величины х определяется как:

, то же для дискретного распределения

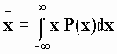
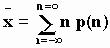
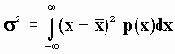
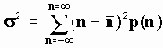
Как уже говорилось, во многих случаях шум имеет гауссово распределение с нулевым средним значением амплитуды. В этих случаях среднее значение мощности шумового сигнала равно вариации функции плотности вероятности. В этом случае отношение сигнал-шум будет равно

. Если шум носит чисто тепловой характер, то s2=kTB. В общем случае s2 = EnB [Вт], где полоса B измеряется в Гц, En энергия шума.

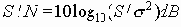
Шум определяет вероятность ошибки при передаче сообщения по каналу связи и, в конечном итоге, пропускную способность канала (см. теорему Шеннона; раздел 2.1 Передача сигналов по линиям связи ).

Содержание Назад Вперед

Forekc.ru
Рефераты, дипломы, курсовые, выпускные и квалификационные работы, диссертации, учебники, учебные пособия, лекции, методические пособия и рекомендации, программы и курсы обучения, публикации из профильных изданий